PRESENTATIONS

                                             

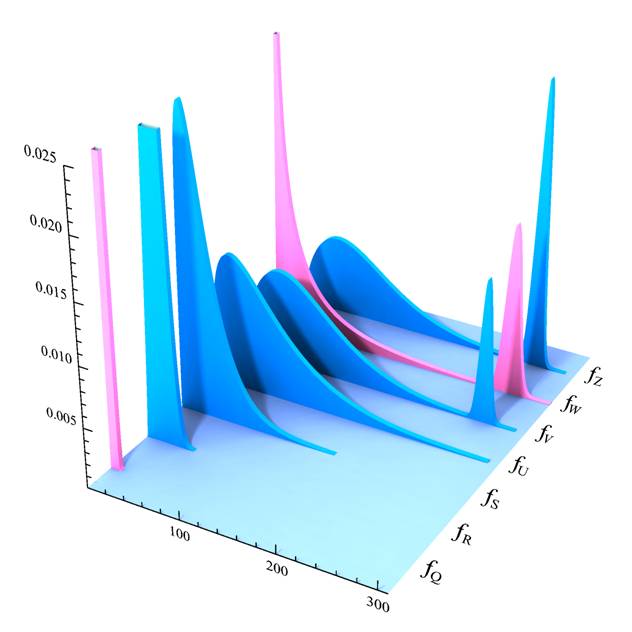Image by Jos Leys from Mathematica® code by author


Probability density functions associated with continuous probability distributions as projections of total developmental potential.  For a population of conceptuses nurtured in enabling circumstances of a given kind, we may recognize as an outcome of a random trial the most advanced instantaneous developmental stage attained by each conceptus.  Where Ω is the set of most advanced stages nomologically possible of attainment in situations of the given kind, E is a σ-algebra over Ω, and P is a probability measure on E, we may define a random variable X: Ω → R assigning to each attainable stage a real number representing the time by which the stage is indexed.  X  induces a P-determined probability distribution with which is associated a probability density function (‘PDF’).  Shown here are PDFs associated with absolutely continuous probability distributions for seven kinds of situation.  The x-axis displays stage indices from 0 to 315 days. ƒQ is a PDF for the tissue culture dish. ƒW, a PDF for the womb, manifests a distribution modeled by a convex combination of Weibull and normal distributions.  Shown in blue are plots of PDFs for imagined artificial uteruses.  Viewing capacity acquisitions mapped to stages as actualizations of potential, each probability distribution may be understood as a projection of total developmental potential, the set of developmental potentials possessed by a member of the population of conceptuses in enabling circumstances of the given kind. The least upper bound of a PDF's support (the closure of the set of points at which the value of the function is nonzero), whose preimage under X is the least upper bound of probable stages, reveals the least upper bound of total developmental potential.